假如AMC数学竞赛有段位,图中可以很明显的看出AMC10数学竞赛处于铂金段位,入门以上,但是还是有一定的难度,那么什么样的基础才能参加AMC10数学竞赛?小编根据AMC10数学竞赛考试特点整理了一些,具体如下:
需要掌握简单计算与应用题、数论、平面几何(多边形与圆)、立体几何、函数方程坐标系、排列组合与统计概率等重点知识。
熟记500以上数学相关的英语单词,并可熟练阅读英语短文。
如果读的是公立学校,需要学完初三和高一公立学校课内知识。
如果学生学的是AP课程,需要学完precalculus(即学习微积分前的必修课程);如果学生学的是IB课程,学生需要学完 DP(即大学预科项目);A-level课程,学生需要学完C1-C2(即基础数学必考的两个单元)。
AMC10数学竞赛的考试内容主要集中在比例、数论、几何、概率和统计等基础的数学知识上,不涉及微积分、三角函数等更高级的数学内容。
代数在AMC10数学竞赛中占据较大比重,主要考点包括函数(一次函数、二次函数等)、方程(一元二次方程、分式方程等)、数列(等差数列、等比数列)以及不等式(一元一次不等式、一元二次不等式)等。
代数部分会出现一些难题,这些题目往往需要学生具备较强的代数变形能力、逻辑推理能力以及综合运用知识的能力。
几何模块的考点包括平面几何图形(三角形、四边形、圆等)的性质、定理以及相关计算,如角度计算、边长计算、面积计算等,还涉及空间几何的一些基础知识,如立体图形(正方体、长方体、圆柱体、圆锥体等)的表面积和体积计算 。
几何部分的难题通常需要学生添加辅助线,将复杂的几何图形转化为熟悉的基本图形,再运用多个几何定理进行综合推导和计算,对学生的空间想象力、逻辑思维能力和解题技巧要求较高。
数论在AMC10数学竞赛中虽然所占比重相对较小,但却是一个重要的知识模块。主要考点包括整数的性质(如整除、余数、奇偶性等)、质数与合数、最大公因数与最小公倍数、同余方程以及一些特殊的数论函数等。
数论问题常常与其他数学知识模块相结合,考查学生的综合运用能力,这也进一步增加了数论问题的难度。


 AMC10/12考后晋级AIME该如何...
AMC10/12考后晋级AIME该如何... 跳过AMC8直接参加AMC10数学...
跳过AMC8直接参加AMC10数学... AMC10竞赛难度分布及AMC...
AMC10竞赛难度分布及AMC... AMC10竞赛难在哪?AMC10竞...
AMC10竞赛难在哪?AMC10竞...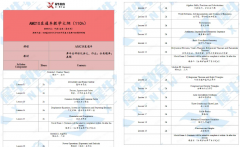 AMC10竞赛考什么?AMC10竞...
AMC10竞赛考什么?AMC10竞...