AMC10数学竞赛考试内容
代数
多项式:涉及多项式的运算、因式分解、余数定理、韦达定理、根与系数的关系等。
方程与不等式:特殊高次方程的求解,进阶不等式、均值不等式的应用。
函数:函数入门知识,包括定义域、值域的求解,二次函数、指数函数、对数函数、简单三角函数的性质和应用。
数列:数列进阶知识,如等差数列、等比数列的通项公式、求和公式的综合运用,以及一些特殊数列的规律和求解方法。
几何
立体几何:点线圆的关系、三维坐标系的应用、立体几何作图,正多面体的性质,欧拉公式的运用,特殊立体几何图形(如三棱锥、圆锥、球等)的表面积、体积计算,以及相关的立体几何技巧。
进阶几何:进阶几何作图,三角形的进阶知识,如正弦定理、余弦定理的应用,内切圆和外切圆的性质,斯图瓦尔特定理,共点和共线问题,圆和四边形的关系,四点共圆的判定和性质,圆的外切四边形的性质,正多边形的角度、周长和面积计算,进阶平面几何技巧,解析几何入门等。
数论
数的基本性质:数、数组和序列的相关知识,整数、分数和小数的性质,进制转换问题。
同余问题:模运算,复杂同余问题的求解,如根据同余的性质求余数。
方程问题:基本丢番图方程的求解,如求满足特定条件的整数解。
组合
计数原理:容斥原理的应用,二项式定理及相关结论。
排列组合:进阶排列、组合问题,如有限制条件的排列组合问题的求解。
概率与期望:概率期望入门知识,如计算简单事件的概率、期望。
其他方法:递推、二分法等进阶组合方法的应用,如通过递推关系求解数列的通项公式。
AMC10数学难度分析
AMC10 数学竞赛试题难度具有多方面的特点,整体呈现出从易到难、知识点融合度高、对思维能力要求强。
前 10 题:通常较为基础,难度相对较低。
主要考查学生对基本数学概念、公式的理解和简单应用。
中间 10 题(11 - 20 题):难度逐渐上升,开始对知识点进行综合考查。
会出现多个知识点的融合,要求学生有更灵活的思维和较强的知识运用能力。
后 5 题(21 - 25 题):属于高难度题目,具有很强的挑战性。
这些题目往往需要学生具备深入的数学洞察力、创新的解题思维和丰富的解题经验。常常会出现一些不常见的数学模型或需要运用特殊的数学技巧来解决,比如涉及到复杂的数论问题,需要运用同余定理、中国剩余定理等高级知识;组合问题可能需要运用容斥原理、递推关系等进行复杂的分析和计算,有时还会出现一些需要通过构造特殊例子或反例来解决的问题。
代数模块:基础的函数、方程问题相对容易,但涉及到高次方程、复杂函数的性质和应用时,难度会大幅提升。
几何模块:简单的平面几何图形计算较易,但立体几何中关于空间想象力的问题,以及平面几何中涉及到四点共圆、相似三角形的复杂应用等内容难度较高。
数论模块:数的整除、余数等基础问题较为简单,但同余方程、不定方程等内容则具有较高难度,需要学生掌握数论的高级定理和方法,并能进行深入的推理和分析。
组合模块:基本的排列组合计数问题难度适中,但当涉及到概率的计算、组合恒等式的证明以及复杂的组合构造问题时,难度会显著增加。



 AMC10数学竞赛新手必看:...
AMC10数学竞赛新手必看:... 上海AMC竞赛培训机构介绍...
上海AMC竞赛培训机构介绍... AMC10/12竞赛与AIME竞赛分数...
AMC10/12竞赛与AIME竞赛分数... 几年级学生适合报考袋鼠...
几年级学生适合报考袋鼠... 深圳学生参加袋鼠数学竞...
深圳学生参加袋鼠数学竞...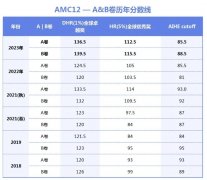 2024年AMC12竞赛AB卷分数线...
2024年AMC12竞赛AB卷分数线... 深圳家长必看:袋鼠竞赛...
深圳家长必看:袋鼠竞赛... 上海【浦东/徐汇/黄浦】...
上海【浦东/徐汇/黄浦】...